Fysikken og kræfterne bag et vertikalt spring

7 minutters læsning

Det vertikale hop er et rigtig godt eksempel på fysikkens love. Her kan du virklig lære noget om sammenhængen mellem hastighed, acceleration, kræfter og svævetid. Det er særlig interessant, når man har adgang til en kraftplatform, som vi har på Vejle Idrætshøjskole.

I dette indlæg kigger vi på fem faser i det vertikale spring, og vi kigger på hvordan de fysiske love virker i de enkelte faser. Jeg har baseret dette indlæg på en rigtig god artikel på www.thehoopsgeek.com.

Kræfter der påvirker springeren

Når du springer, så vil du i dit afsæt påvirke jorden med den kraft du kan sætte af med. Men samtidig vil jorden påvirke dig med de modsatrettede kræfter.

Fænomenet er beskrevet i Newtons love, og mest præcist Newtons 3. lov.

Et legeme a, der påvirker et legeme b med en kraft, vil blive påvirket med en lige stor modsat rettet kraft.

— Wikipedia

Så når du påvirker jorden med en bestemt kraft, så vil du blive påvirket af en lige så stor modsatrettet kraft.

Analyse på kraftplatform

Det er derfor du kan bruge en kraftplatform til at analysere spring. På kraftplatformen kan du se, hvor meget kraft, hvor hurtigt og hvor længe atleten udøver kraft.

I denne Youtube-video kan du se et eksempel på et spring og se de målte kræfter i forhold til springet.

video til Fysikken og kræfterne bag et vertikalt spring

I denne Youtube-video kan du få en god gennemgang af, hvad der sker i hoppet.

Analyse af kræfterne i det vertikale hop

I det følgende kigger vi på relationerne mellem kraften, accelerationen, hastigheden og højden af et vertikalt spring. Vi tager udgangspunkt i en kraftplatformanalyse, fordi det er et godt eksempel på, hvordan fysikkens love kan ses i praksis i et spring.

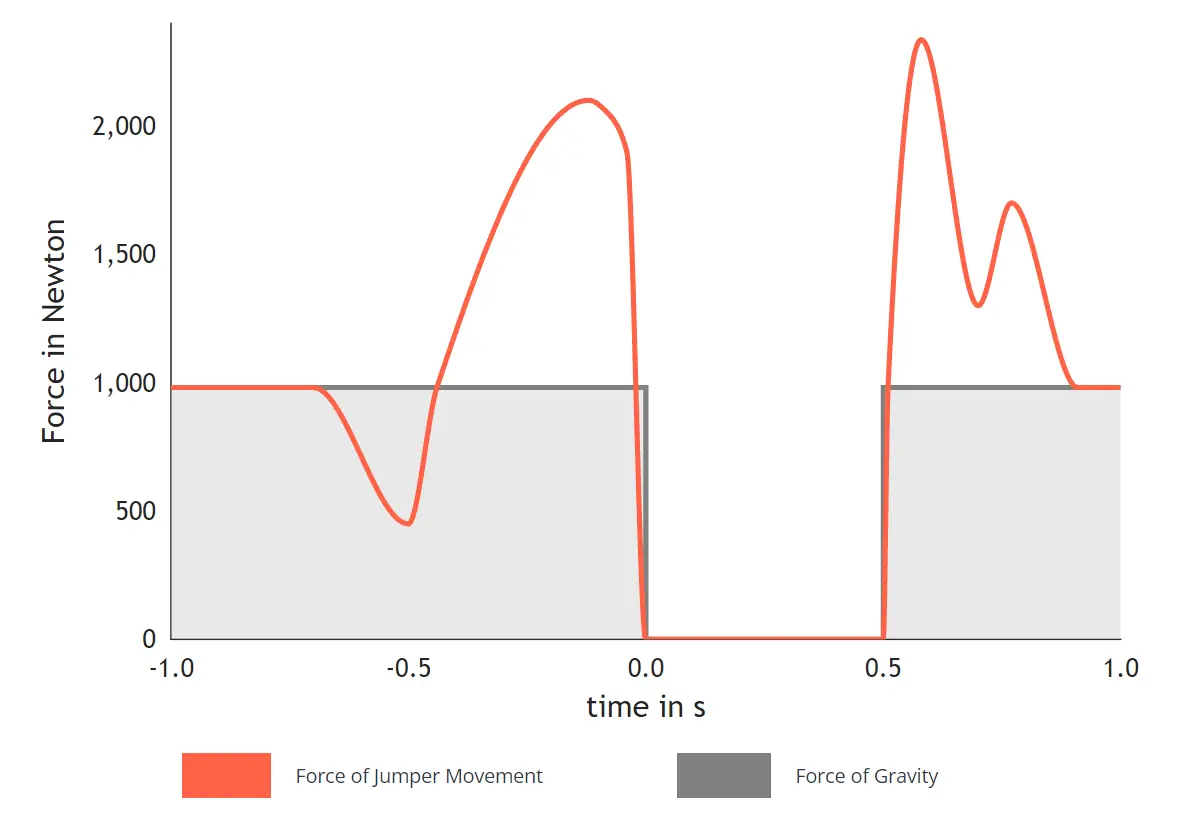
Fase 1. Før hoppet

Før hoppet kan man se, at kraftplatformen påvirkes af en lige linje, som har en kraft på 981 Newton. Atleten bevæger sig ikke endnu, så hvor kommer denne kraft fra?

Det er naturligvis tyngdekraften, der trækker atleten ned mod jorden. Kraften er forklaret i denne formel.

$F = m * g$

Her er m atletens masse, og g er accelerationen fra tyngdekraften.

F er den kraft, som atleten bliver nødt til at overkomme bare for at neutralisere tyngdekraften og bevæge sig overhovedet. Vi ved at g er lig med 9,81 m/s². Derfor kan vi opstille følgende formel:

$981 N = m * 9.81 m/s^2 \\ \\ => m = \frac{981N}{9.81 m/s^2} = 100kg$

Inden atleten bevæger sig er kraftplatformen egentlig en en simpel vægt, som fortæller størrelsen af kraften, som tyngdekraften påvirker atleten med.

Fase 2. Nedadgående bevægelse før hoppet

1. Acceleration i nedadgående bevægelse

I denne fase er der en nedadgående bevægelse, hvor atleten bøjer i knæene og gør sig klar til at springe ved at sænke tyngdepunktet. Nu registrerer kraftplatformen kræfter, som er mindre end tyngdekraften. Det betyder, at atleten har en nedadgående acceleration.

Det kan beskrives med denne formel:

$F_{Jumper} = F_{GRF} - F_{Gravity}$

Det er interessant, når man analyserer et hop, hvor hurtigt den nedadgående bevægelse foregår. Kan vi beregne det fra resultaterne fra kraftplatformen?

Vi ved:

$F = m a => F t = m a t$

F er ikke konstant undervejs, men en funktion af tiden og v = a * t. Det giver os følgende formel:

$=> \int_{t_1}^{t_2} F_{Jumper}(t) \mathrm{d}t = m v$

Her er F_Jumper(t) er forskellen mellem de registrerede kræfter fra jorden og tyngdekraften. Dette kan udregnes fra data på kraftplatformen. Det nedadgående impuls er altså området under tyngdekraften.

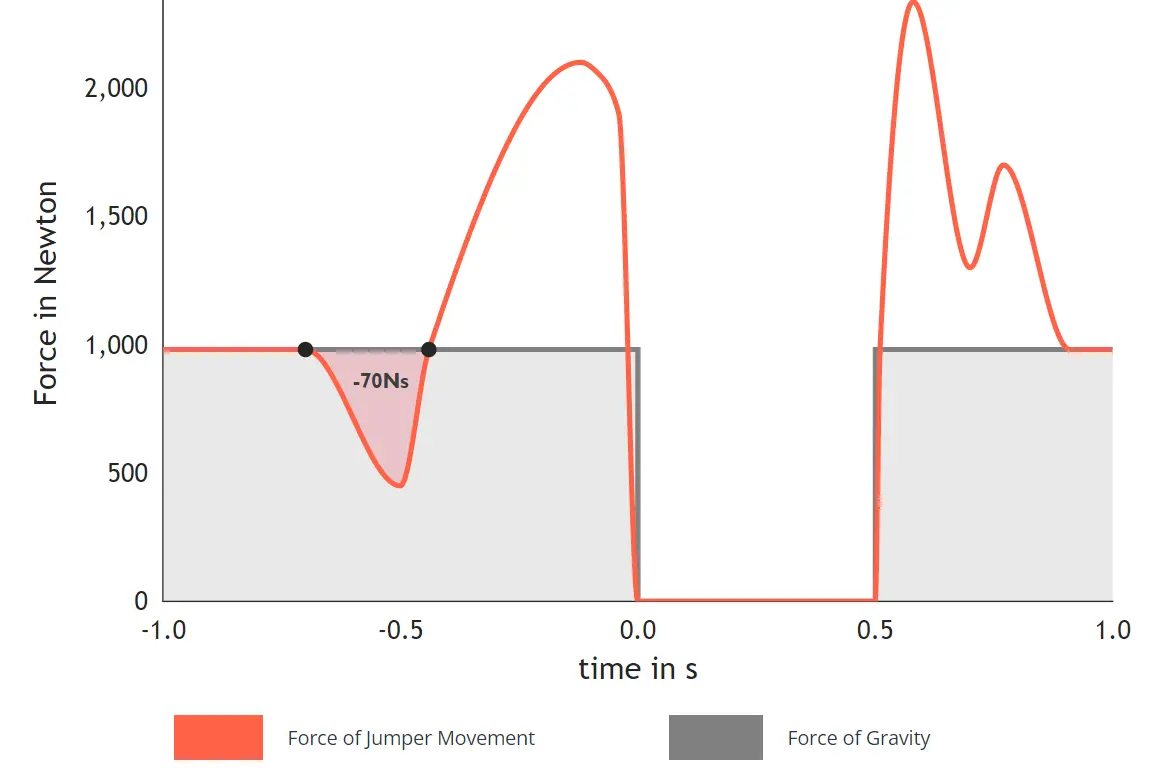
Hvis vi antager at impulset bliver -70 Ns, så kan vi konkludere at:

$\int_{t_1}^{t_2} F(t) \mathrm{d}t = m v \\ \\ \\ => -70 N s = 100kg * v \\ \\ \\ => v = -70 N s / 100kg = -0.7 m/s$

Atleten opnår altså den højeste hastighed på -0,7 m/s i den nedadgående bevægelse før hoppet.

2. Deceleration af den nedadgående bevægelse

Indtil nu har vi kigget på forspændingen i hoppen i den nedadgående acceleration. Det er let at identificere denne fase, som ligger under tyngdekraften.

Atleten er nødt til at decellere den nedadgående bevægelse for at opnå en ganske kort pause nederst i forberedelsen til afsættet.

Decelerationen af bevægelsen er lidt vanskeligere nøjagtigt at finde, men hvordan identificerer vi den i grafen fra kraftplatformen?

I den nedadgående bevægelse oparbejdede vi et impuls på -70 Ns. Nu skal vi finde et impuls i den modsatte retning. Vi kan beskrive impulset sådan her:

$\int_{t_2}^{t_3} F_{Jumper}(t) \mathrm{d}t = 70 Ns$

F(t) og t₂ er kendte. Nu kigger vi efter t₃, hvor impulset er lig med 70 Ns.

Det kan illusteres i grafen, hvor vi kigger efter t₃, så vi har et område under grafen, som også er 70 Ns.

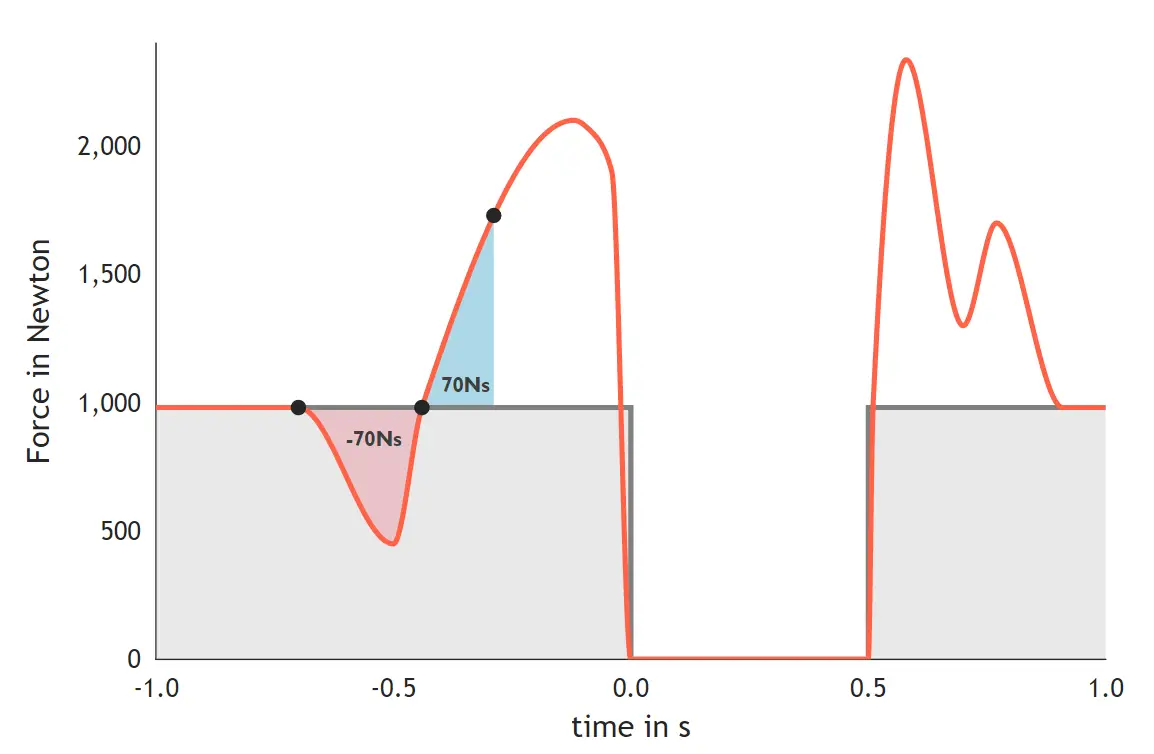
Fase 3. Opadgående bevægelse før afsættet

Denne fase begynder i bunden af hoppet lige som atleten begynder at sætte af med en kraftfuld bevægelse opefter. I grafen kan du se, at atleten kort efter at have været på det laveste sted i hoppet opnår de højeste kræfter. Accelerationen fortsætter opefter indtil fødderne forlader platformen, og der ikke længere kan måles kræfter i platformen.

$\int_{t_3}^{t_4} F_{Jumper}(t) \mathrm{d}t = m v$

Dette integral kan illustreres som det gule område i målingen fra kraftplatformen.

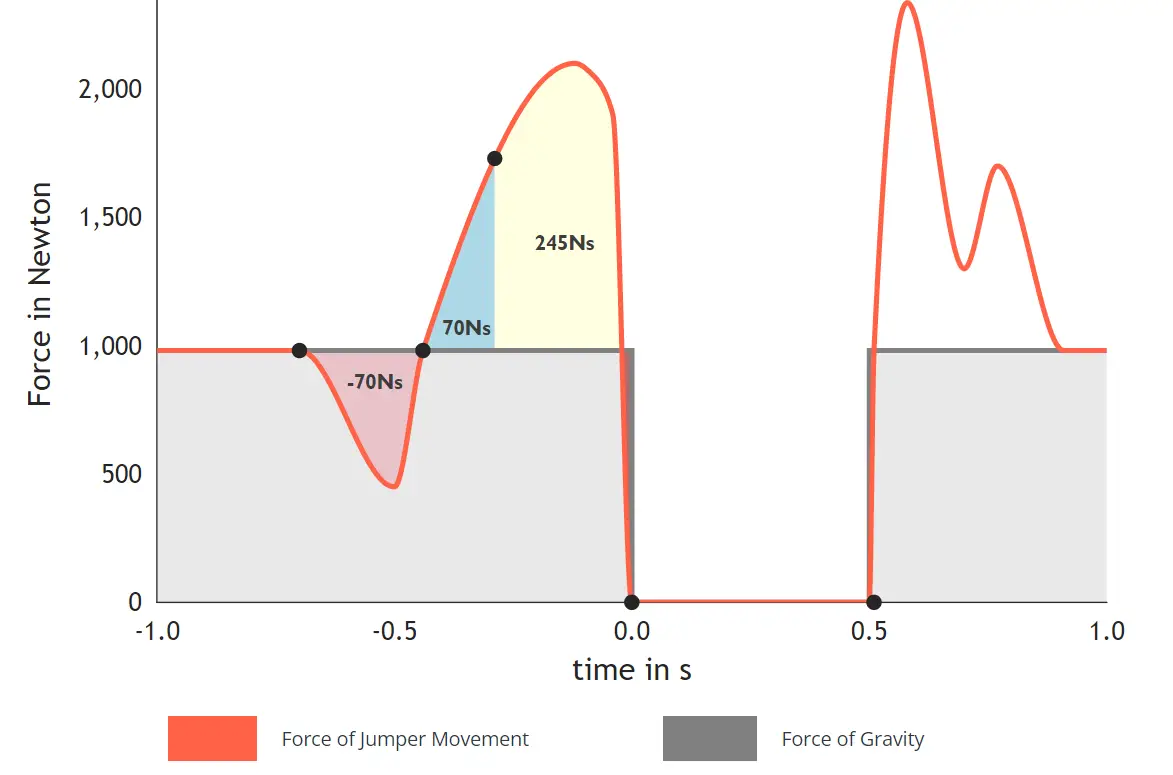
Dette område kan i dette eksempel udregnes til 245 Ns. Derfor kan vi udregne afsætshastigheden til:

$245 N s = 100kg * v \\ \\ \\ => v = 245 N s / 100kg = 2.45 m/s$

Fase 4. Svævefasen

I denne fase kan atleten ikke længere påvirke tyngdepunktet. Højden af hoppet er nu forudbestemt af den hastighed atleten kunne bygge op under afsættet. Den eneste kraft der virker på atleten er nu tyngdekraften.

Når nu atleten ikke længere kan påvirke tyngdepunktet. Så kan vi estimere den samlede hoppehøjde. Vi kender v(0)=2.45 m/s² og vi kender tyngdekraften på a=9.81m/s².

Vi ved også, at hastigheden i toppen af hoppet nødvendigvis må være 0, ellers ville atleten jo blive ved med at komme højere og højere op.

$v(t_{peak})=0$

Når vi kender hastigheden ved afsættet og tyngdekraften, så kan vi udregne hastigheden på alle tidspunkter i i hoppet sådan her.

$v(t)=v(0) -a * t$

Derfor kan vi også udregne, hvornår springeren er på det højeste punkt i springet (hvor hastigheden er 0).

$v(t_{peak}) = v(0) - a * t_{peak} \\ \\ => 0 = v(0) - a * t_{peak}$

$=> t_{peak} = \frac{v(0)}{a} = \frac{2.45m/s}{9.81m/s^2} = 0.25s$

Når vi kender hastigheden v(t) på hvert tidspunkt af hoppet, og vi kender tiden inden springeren er på det højeste punkt i hoppet efter 0,25 sekunder, så kan vi udregne hoppehøjden som et integral af hastigheden over den tid, det tager at opnå det øverste punkt i springet.

$h_{jump} = \int_0^{\frac{v(o)}{a}} \bigg( v(o) - at \bigg) \ \mathrm{d}t= \\ \\= v(o)t \ - \ \frac{1}{2} at^2 \ \bigg|_0^{\frac{v(0)}{a}} \\ \\= v(0) \left(\frac{v(0)}{a}\right) - \frac{1}{2} a \left(\frac{v(0)}{a}\right)^2 \\ \\= \frac{v(0)^2}{a} \ - \ \frac{1}{2} \frac{v(0)^2}{a} \\ \\$

$=> h_{jump} \ = \ \frac{1}{2} \frac{v(0)^2}{a}$

Nu ender vi altså med en relativt simpel formel, som gør det muligt at beregne den vertikale hoppehøjde, hvis vi kender afsætshastigheden. I vores specifikke eksempel får vi:

$h_{jump} = \frac{1}{2} \frac{(2.45m/s)^2}{9.81 m/s^2} = 0.306m$

Du kan bruge denne beregner:

Hvis du har en kraftplatform, så kan du altså relativt enkelt udregne hoppehøjden ud fra den indledende hastighed. Men er der andre måder du kan bruge fysik til at udregne din hoppehøjde.

Udregn hoppehøjden fra svævetiden

Hvis du ikke kender kræfterne ved afsættet eller den oprindelige hastighed ved afsættet. Vi kender i stedet springerens svævetid, så kan vi bruge svævetiden i stedet.

Det er noget lettere at finde udstyr, som kan hjælpe os med at måle svævetiden. Vi kan enten få svævetiden fra en hoppemåtte eller ved at måle svævetiden med et high speed kamera eller en smartphone. Det er bl.a. den teknologi, som bruges i The Hoops Geek online måleinstrument.

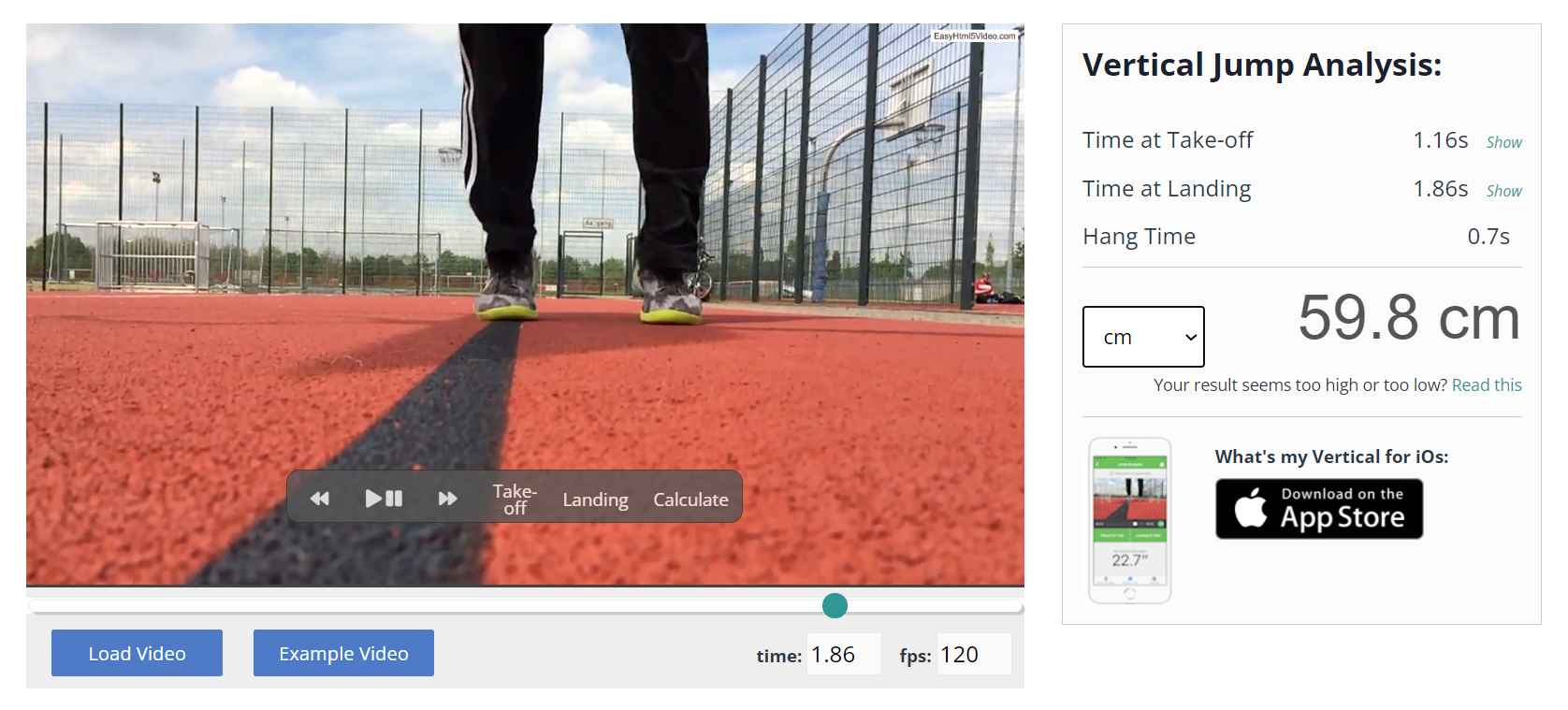
Du kan bruge The Hoops Geek onlineredskab til at måle hoppehøjde ud fra en video baseret på svævetiden.

I vores eksempel blev svævetiden udregnet til t = 0,5 s, men den kunne vi også aflæse.

Da vi kan udregne hoppehøjden for et spring, når vi kender den oprindelige hastighed ved afsætstidspunktet med denne formel.

$=> h_{jump} = \frac{1}{2} \frac{v(0)^2}{a}$

Hvis vi kan finde den oprindelige hastighed ved et spring, som har en svævetid på 0,5 sekunder, så kan vi altså udregne hoppehøjden. Hvis du springer 1 meter, så betyder det også, at du skal falde en meter igen efter, at du har opnået toppunktet i springet.

Hastigheden er en lineær funktion (v=a * t). Derfor opnår springeren toppunktet nøjagtigt i midten af springet. Det giver os følgende sammenhæng:

$t_{peak} = 0.5 * t_{hangtime}$

Så hvis vi gerne vil vide, hvor højt en med en svævetid på 0,5 sekunder hoppede, så skal vi bare udregne hvor langt et fritfaldende objekt falder i halvdelen svævetiden. Personen falder altså ned mod jorden igen på halvdelen af 0,5 sekunder, nemlig 0,25 sekunder.

Den generelle formel for fritfaldende objekter er:

$S = \int_0^{\frac{1}{2} t_{hangtime}} v(t) \; dt \\ \\ = \int_0^{\frac{1}{2} t_{hangtime}} a * t \; dt \\ \\ = \frac{1}{2} a t^2 \; \bigg|_0^{\frac{1}{2}t_{hangtime}} \\ \\ = \frac{1}{2} a \left( \frac{1}{2} t_{hangtime} \right)^2 \\ \\ = \frac{1}{8} a \: t_{hangtime}^2 \\ \\$

I vores specifikke eksempel med en svævetid på 0,5 sekunder får vi følgende resultat:

$S = \frac{1}{8} a \: t_{hangtime}^2 = \frac{1}{8} * 9.81m/s^2 * 0.5^2 = 0.306m$

Hvis du kan finde din svævetid, så kan du altså udregne din hoppehøjde.

Fase 5. Landingen

I afsættet skaber atleten en kraft, som er stor nok til at overkomme tyngdekraften, så vedkommende letter fra jorden. Vi har før vist, at hastigheden på toppunktet er 0 m/s, og det er let at vise, at hastigheden i landingen er den samme som i afsættet, men i den modsatte retning.

$\int_{t_4}^{t_5} F(t) \mathrm{d}t = m v(t_4) = m v(t_0)$

Impulset kan ses i den grønne del af grafen nedenunder.

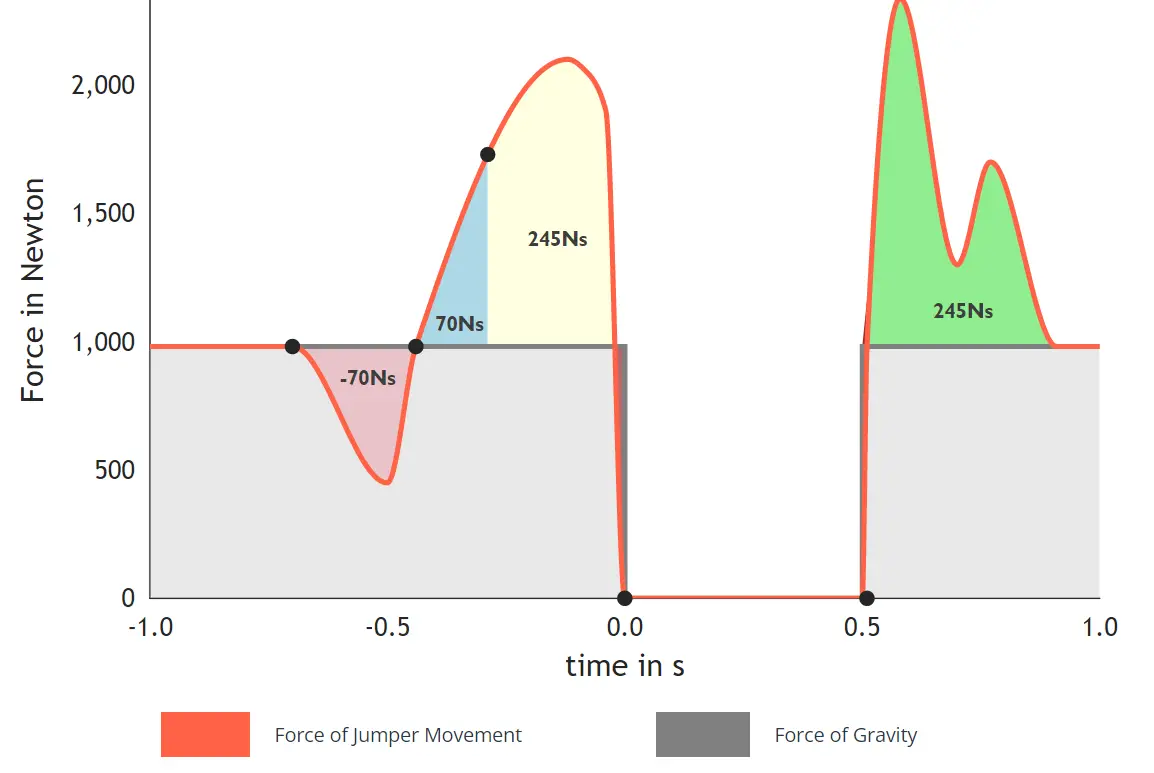
I vores eksempel har atleten accelereret fra en hastighed på v(t₀) = 0 til v(t₃) = 2.45 m/s² under afsættet. Under landingen skal atleten accelere fra en hastighed på v(t₄) = -2.45m/s² til en hastighed på v(t₅)=0m/s².

Ændringen i hastighed v_delta = 2.45m/s² er den samme i begge tilfælde, så impulset skal også være det samme. Det kan ses i grafen, at både det gule og grønne område er 245 Ns.

Nu står atleten igen stille efter hoppet, og de fem faser i hoppet er overstået.